Modélisation des liaisons mécaniques

par cfaury · Publié 6 janvier 2019 · Mis à jour 16 janvier 2024

\(\newcommand{\indiceGauche}[2]{{\vphantom{#2}}_{#1}#2}\)

Notions de Mécanisme et de Solides

On appelle mécanisme, un ensemble de pièces mécaniques reliées entre elles par des liaisons, en vue de réaliser une fonction déterminée.

Nous admettrons que les pièces mécaniques peuvent être modélisées par des solides indéformables.

Exception : les pièces dont la fonction est de se déformer (ressorts, joints, etc…)

Exemple de mécanisme : un micromoteur de modélisme

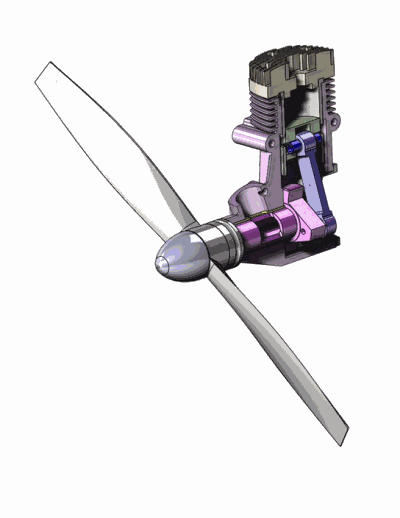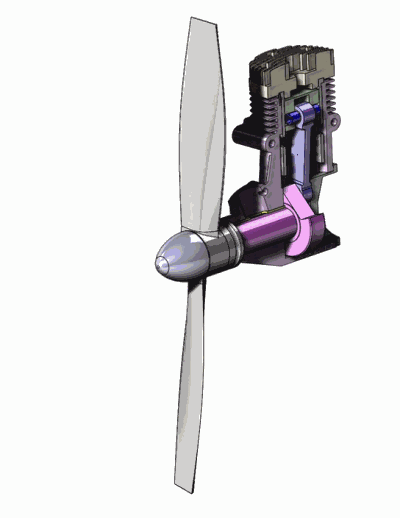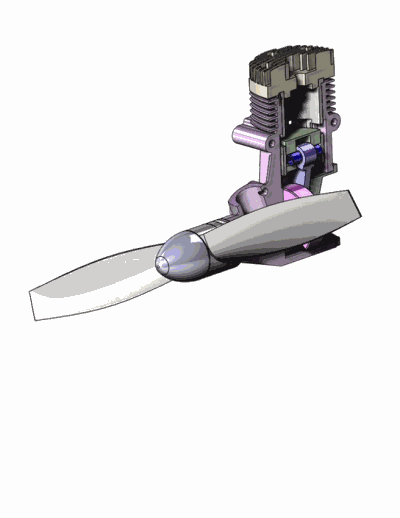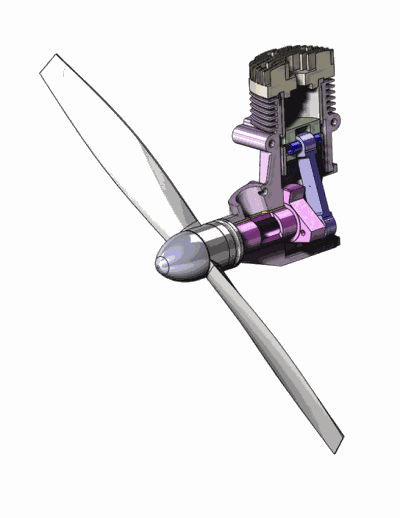
Solide indéformable

Le solide indéformable possède une masse constante et un volume dont les limites sont invariantes quelles que soient les actions extérieures auxquelles il est soumis.

Conséquence géométrique : la distance entre deux points quelconques d’un solide indéformable est invariable.

Exemple : la bielle du micromoteur est supposée indéformable ⇔ la distance entre ses points \(A\) et \(B\) est constante

Paramétrage de la position d’un solide

Pour connaitre la position de tous ses points dans l’espace, il suffit de connaitre la position d’un repère lié à ce solide.

Notons \(\mathcal{R}(O, \vec{x}, \vec{y}, \vec{z})\) le repère de référence
et \(\mathcal{R}(O_1, \vec{x_1}, \vec{y_1}, \vec{z_1})\) le repère lié au solide.

La position du solide dans l’espace, est déterminée par 6 paramètres indépendants :

Position du point \(O_1\) dans \(\mathcal{R}\) : 3 coordonnées
Orientation de \((\vec{x_1}, \vec{y_1}, \vec{z_1})\) par rapport à \((\vec{x}, \vec{y}, \vec{z})\) : 3 angles

Exemple : repère local lié au solide 2 (la bielle) et repère de référence, lié au solide 0 (le bâti)

Degré de liberté d’un solide

On appelle « libertés » d’un solide par rapport à un référentiel, les mouvements indépendants de ce solide pour passer d’une position à une autre.

Il existe deux mouvements élémentaires entre les solides :

Le mouvement de TRANSLATION (RECTILIGNE) : les trajectoires de tous les points du solide sont des droites parallèles.
Le mouvement de ROTATION : les trajectoires de chaque point sont des cercles coaxiaux.

Attention : pour définir un mouvement, il est nécessaire de fixer une référence. La notion de mouvement est toujours relative : c’est le mouvement d’un système par rapport à un référentiel (ici défini par le repère \(\mathcal{R}\)).

On dit que le solide possède des degrés de liberté, chacun contrôlés par :

Soit un paramètre de position linéaire = translation
Soit un paramètre de position angulaire = rotation

Par exemple, dans un repère \(\mathcal{R}(O, \vec{x}, \vec{y}, \vec{z})\), on pourra les noter :

Tx, Ty, Tz, pour translations selon les axes \(\vec x\), \(\vec y\) et \(\vec z\)
Rx, Ry, Rz, pour rotations autour des axes \(\vec x\), \(\vec y\) et \(\vec z\)

Remarque : un solide possède au maximum 6 degrés de liberté et au minimum 0.

Notion de liaison

On appelle liaison entre deux solides l’ensemble des couples de surfaces en contact entre ces deux solides, visant à diminuer la mobilité entre ces deux solides.

La liaison entre 2 solides est définie par la nature et la position de la zone (ou des zones) de contact, elle renseigne sur :

les mouvements relatifs rendus impossibles par ce contact : des degrés de liberté sont supprimés.
les actions mécaniques (forces et couples) transmissibles par ce contact.

Zones de Contacts

Le solide parfait est une masse de matière occupant un volume indéformable, donc délimité par une surface indéformable. Une partie de cette surface peut être constituée de points communs à la surface d’un autre solide : c’est le contact.

Contact ponctuel

Contact linéique

Contact surfacique

Activité

Déterminer la nature de la zone de contact entre :

une sphère dans un cylindre creux de même diamètre
deux cylindres d'axes parallèles
deux cylindres d'axes perpendiculaires
un cylindre dans un cylindre creux de même diamètre

Correction

Sphère dans cylindre : contact linéique (ligne circulaire)

2 cylindres d’axes parallèles : contact linéique (ligne droite)

2 cylindres d’axes perpendiculaires : contact ponctuel

2 cylindres coaxiaux : contact surfacique (surface cylindrique)

Repère local lié à la liaison

C’est un repère orthonormé direct, choisi de manière à caractériser le plus simplement possible la géométrie du contact entre les deux solides, noté \(\mathcal{R}(O, \vec{x}, \vec{y}, \vec{z})\); où \(O\) est le centre géométrique du contact, et les vecteurs \(\vec{x}, \vec{y}, \vec{z}\) sont orientés dans les directions privilégiées tenant compte des symétries du contact.

Remarque : on observera avec attention les repères locaux choisis pour les liaisons usuelles !

Degrés de liberté/de liaison d’une liaison

Les degrés de liberté d’une liaison sont les déplacements élémentaires indépendants autorisés par cette liaison.

On les note :

Tx pour « translation suivant \(\vec x\) »
Rx pour « rotation autour de \(\vec x\) »

Les degrés de liaison sont les déplacements élémentaires interdits par la liaison.

Remarque : Nombre de degrés de liberté + Nombre de degrés de liaison = 6

Liaisons usuelles

Les cas les plus courants de liaison sont répertoriés par une Norme, qui fournit à chaque liaison normalisée : un nom et des symboles de représentation (schéma) dans le plan et en perspective.

Toute description d’une liaison doit préciser en plus du nom de la liaison, toutes les caractéristiques nécessaires à son positionnement dans l’espace : éléments géométriques (points, vecteurs, …) ou paramètres intrinsèques.

Nom de la liaison caractéristiques	Symbole perspective	Symboles plans	Torseur cinématique \(\{ \mathcal{V} (S_1/ S_2) \}\)
Sphère-Plan de normale \(\left(P,\vec x\right)\)			\( {\vphantom{\left\{ \begin{array}{ccc} \\ \\ \\ \end{array} \right\}}}_{\mbox{P}} \left\{ \begin{matrix}{} \omega_{x} & 0\\ \omega_{y} & v_{y}\\ \omega_{z} & v_{z}\\ \end{matrix} \right\}_{\left(\vec x, \vec y, \vec z\right)} \)
Appui-Plan de normale \(\vec x\)			\( {\vphantom{\left\{ \begin{array}{ccc} \\ \\ \\ \end{array} \right\}}}_{\mbox{P}} \left\{ \begin{matrix}{} \omega_{x} & 0\\ 0 & v_{y}\\ 0 & v_{z}\\ \end{matrix} \right\}_{\left(\vec x, \vec y, \vec z\right)} \)
Sphère-Cylindre d’axe \(\left(P,\vec x\right)\)			\( {\vphantom{\left\{ \begin{array}{ccc} \\ \\ \\ \end{array} \right\}}}_{\mbox{P}} \left\{ \begin{matrix}{} \omega_{x} & v_{x}\\ \omega_{y} & 0\\ \omega_{z} & 0\\ \end{matrix} \right\}_{\left(\vec x, \vec y, \vec z\right)} \)
Sphérique de centre \(P\)			\( {\vphantom{\left\{ \begin{array}{ccc} \\ \\ \\ \end{array} \right\}}}_{\mbox{P}} \left\{ \begin{matrix}{} \omega_{x} & 0\\ \omega_{y} & 0\\ \omega_{z} & 0\\ \end{matrix} \right\}_{\left(\vec x, \vec y, \vec z\right)} \)
Sphérique à doigt de centre \(P\) et de rotation interdite \(\vec x\)			\( {\vphantom{\left\{ \begin{array}{ccc} \\ \\ \\ \end{array} \right\}}}_{\mbox{P}} \left\{ \begin{matrix}{} 0 & 0\\ \omega_{y} & 0\\ \omega_{z} & 0\\ \end{matrix} \right\}_{\left(\vec x, \vec y, \vec z\right)} \)
Cylindre-Plan de normale \(\vec x\) d’arête \(\left(P,\vec y\right)\)			\( {\vphantom{\left\{ \begin{array}{ccc} \\ \\ \\ \end{array} \right\}}}_{\mbox{P}} \left\{ \begin{matrix}{} \omega_{x} & 0\\ \omega_{y} & v_{y}\\ 0 & v_{z}\\ \end{matrix} \right\}_{\left(\vec x, \vec y, \vec z\right)} \)
Pivot-Glissant d’axe \(\left(P,\vec x\right)\)			\( {\vphantom{\left\{ \begin{array}{ccc} \\ \\ \\ \end{array} \right\}}}_{\mbox{P}} \left\{ \begin{matrix}{} \omega_{x} & v_{x}\\ 0 & 0\\ 0 & 0\\ \end{matrix} \right\}_{\left(\vec x, \vec y, \vec z\right)} \)
Pivot d’axe \(\left(P,\vec x\right)\)			\( {\vphantom{\left\{ \begin{array}{ccc} \\ \\ \\ \end{array} \right\}}}_{\mbox{P}} \left\{ \begin{matrix}{} \omega_{x} & 0\\ 0 & 0\\ 0 & 0\\ \end{matrix} \right\}_{\left(\vec x, \vec y, \vec z\right)} \)
Glissière de direction \(\vec x\)			\( {\vphantom{\left\{ \begin{array}{ccc} \\ \\ \\ \end{array} \right\}}}_{\mbox{P}} \left\{ \begin{matrix}{} 0 & v_{x}\\ 0 & 0\\ 0 & 0\\ \end{matrix} \right\}_{\left(\vec x, \vec y, \vec z\right)} \)
Hélicoïdale d’axe \(\left(P,\vec x\right)\) de pas \(p\)			\( {\vphantom{\left\{ \begin{array}{ccc} \\ \\ \\ \end{array} \right\}}}_{\mbox{P}} \left\{ \begin{matrix}{} \omega_{x} & v_{x}=\omega_{x}\frac{p}{2\pi}\\ 0 & 0\\ 0 & 0\\ \end{matrix} \right\}_{\left(\vec x, \vec y, \vec z\right)} \)